前言
其实这篇blog只是用来测试图床和Latex在我的博客上的显示效果,题目本身不难,个人认为大约是联赛第二题难度。
题目
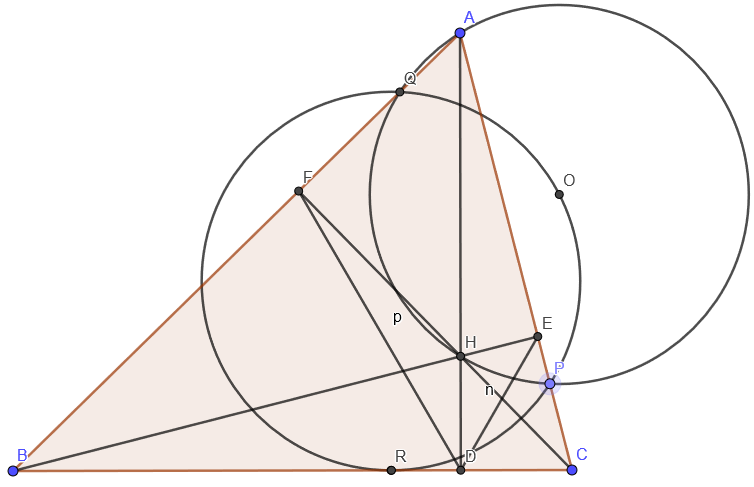
已知锐角三角形$\triangle$ABC的三条高AD,BE,CF交于点H,$\odot$O过点A,H,且分别与边AB,AC交于异于点A的点Q,P。若$\triangle$OPR的外接圆与边BC切于点R,求证:$\frac{CR}{BR}=\frac{DE}{DF}$。
解答
首先,我们容易知道$\angle PRQ=180^{\circ}-\angle POQ=180^{\circ}-2\angle BAC$,下面我们利用同一法来证明:
R点满足R,H,P,C以及R,H,Q,B这两组点分别四点共圆,也就是说点H为P,Q,R三点关于$\triangle$ABC的Miquel点。$\cdots \cdots (*)$
假设R’在BC上且$\angle HRC=\angle APH$,显然,R’是P,Q,R三点关于$\triangle$ABC的Miquel点。那么就有$\angle FR’E$ $=\angle HR’E$ $+ \angle HR’F$ $=\angle HCP$ $+ \angle HBQ$ $=(90^{\circ}$ $- \angle BAC)$ $+ (90^{\circ}$ $- \angle BAC)$ $=180^{\circ}-2\angle BAC$ $=\angle FRE$,这说明点R’在$\odot$OPQ上,而$\odot$OPQ与直线BC相切,所以R=R’,这就证明了(*).
又由于$\odot$OPQ与BC相切,利用R,H,P,C以及R,H,Q,B这两组点分别四点共圆可得$\angle RQP$ $=\angle RQH$ $+ \angle PQH$ $=\angle HBC$ $+ \angle HAC$ $=180^{\circ}$ $- 2\angle ACB$ $=\angle DFE$,同理$\angle RPQ$ $=\angle DEF$,因此$\triangle DEF\sim\triangle RPQ$。则有$\frac{DE}{DF}=\frac{RP}{RQ}\cdots \cdots (**)$。
又$\angle PRC$ $=\angle RQP=180^{\circ}$ $- 2\angle ACB$,所以$\angle RPC$ $=180^{\circ}$ $- \angle ACB$ $- \angle PRC$ $=180^{\circ}$ $- \angle ACB$ $- (180^{\circ}$ $- 2\angle ACB)$ $=\angle ACB$,则RC=RP,同理RB=RQ,结合(**)可得$\frac{CR}{BR}$ $=\frac{RP}{RQ}$ $=\frac{DE}{DF}$,这就证明了原题。